How to build the promised ve(3,3)
Disclaimer: this is not supposed to be used in production. I am writing it only because I found it interesting.
Recap:
If you have not read my previous thread, please take a look.

From the thread, we learned two things about ve(3,3):
Weekly emission always = weekly emission cap. % Locked does not matter. No deflation behavior.
APR of locking token is always the same,
2mm/Nwhich is the inflation rate, and does not depend on other users’ locking behavior. No (3,3).
Although AC’s design does not achieve it, I want to give it a shot to come up with a simple incentive design that works like the promised ve(3,3).
Laying the brick work
Let’s establish what we want to build first. We want to achieve two things, which is what ve(3,3) promised:
If more % of token locked, the total emission goes down.
If I lock and you lock, we both get higher APR than if only one of us lock. Therefore, collaboration wins (3,3).
Then let’s abstract some assumptions we previously had:
Current total supply = N. It is the current supply of all the locked tokens + liquid tokens.
% of token locked = x. (# of locked token) / N, represented as a number between 0 and 1, exclusive.
Weekly emission cap: C = f(N,x). The maximum emission per week. C is a function of the current total supply N and the current lock rate x. f(N,x) is inverse to x. The higher lockup rate, the lower emission cap.
Weekly emission to pools: P = g(C,x). Emission goes to two places, the pools (or in whatever place the protocol incentives its users) and the ve locker. The weekly emission to the pool P is a function of the weekly emission cap C and the % token locked x. The more locking there is, the more emission goes to the ve lockers.
Calculating payouts
So, with these new functions and abstractions, we can add this into our table.
Just to quickly go over how each cell is calculated:
First calculated the Pool column and find total future token amount.
Then find the future locked amount.
Lastly fill in the emission to the locked pool.
From the table we can extract another interesting relationship that is:
Now, we can replace all the P’s in terms of C, we calculated the table below:
We simplify it a bit:
Now it looks a lot better.
Going back to our goals:
When x increases, C decreases.
When x increases, weekly APR for locking* increases.
*weekly APR for locking = rewards / principle = C * x / (x * N) = C / N
In terms of math, in order to satisfy these two assumptions, we want:
WOAH! These two statements are contradicting each other…
Since N is not a negative number (you cannot have negative balance), it is not possible to satisfy these two statements at the same time.
Therefore, based on AC’s article. It is not possible to achieve ve(3,3) given the ratio between the ve locker and the pools is constant.
Thinking outside the box
Although it is not possible to have exactly what AC proposed, we can see that the first requirement is quite easy to satisfy.
When x increases, C decreases.
If the dC/dx is less than 0, when x is between 0 and 1, we can satisfy the first part.
The second part is the harder part.
When x increases, weekly APR for locking increases.
This is hard because we have to keep the non-dilution condition for ve tokens. If we think about this concept abstractly: when you lock your token, your token will not be diluted. Therefore, other people’s behavior will not influence your payoff at all. Everyone will keep their same share.
So the (3,3) mentality of working together cannot coexist with the non-dilution condition.
But this is where it gets interesting. What if instead of saying ve locker never gets diluted, we propose that ve locker only get diluted when less than y% of token are locked. Therefore we will push the lock rate to y% because as more people lock into the vault, the more APR everyone will have. (3,3)
Notations and constraints:
Current % of token locked = x
Current total supply = N
Current locked supply = N * x
Current circulating supply = N * (1-x)
Total weekly emission: C := f(N,x)
dC/dx < 0
Emission to ve locker: L := f(C,x)
dL/dx > 0
Emission to pool (circulating): P = C - L
dP/dx < 0
With these conditions in mind, I will draw out the corresponding curves for the ve(3,3) model presented above. There are many ways to achieve this and I am just showing one possibility.
Relationship between C and x:
The graph above represents the relationship between weekly emission and % of token locked in the system. There are two features of the curve:
At x = 0, total weekly emission is at max. At x= 100%, emission is at a predetermined min.
Slope of the line is always negative.
The graph above represents the relationship between % of token locked and the ratio of (Weekly Emission in locker) / (Total Weekly Emission), L / C. I also draw the dotted black line with a slope of one.
When L/C is below the dotted black line, it means the ve locker is being diluted. And when L/C is above the dotted black line, the ve locker’s share is increasing at a faster pace than the overall emission.
This relationship aims to
Bootstrap initial locking percentage by making locking’s yield attractive.
After % token locked reach a certain threshold, it becomes a game of (3,3) where the marginal locked token will increase the yield for everyone. No more yield dilution.
After reaching a predetermined locked percentage, in this case 80%, the ve locker will no longer be diluted. The end of (3,3) but no dilution happens.
If you want to be comprehensive, you can also make total weekly emission decrease with respect of time. Therefore, your emission schedule is inflating at a decreasing rate with respect to time.
Summary
The original ve(3,3) does not live to its promise because of the conflicting constraints it imposed on itself. However, by tweaking the constraints a little bit, we can make ve(3,3) possible. In this simple design, the system incentivizes people to lock their tokens together to a predetermined threshold. At the same time, emission is curbed by the locked token.
I am not sure how this will be used or whether this should be used. But this method introduces some interesting dynamic into the ve model.



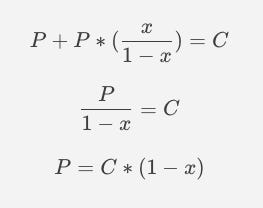






What happens to all of these locking models when people come up with an easy way to sell/trade wallets/seed phrases ?